세그먼트 트리
세그먼트 트리는 배열의 데이터에 대한 구간 질의(구간합, 최대,최소, 구간곱),
배열 값 업데이트를 빠르게 수행하기 위해 고안해 낸자료구조이다.
세그먼트 트리는 완전 이진 트리로 구현한다.
세그먼트 트리 이해하기
샘플 데이터 {5, 8, 4, 3, 7, 2, 1, 6}가 있다. N = 8 (배열의 크기, 트리배열의 크기도 8이다)
그리고 그 샘플 데이터로 만든 배열 위에 세그먼트 트리를 그려보았다.

질의 결과 값 구하기
i=1부터 시작한다고 가정했을 때, i=3~7까지의 합이 구간 질의로 주어졌다고 하자.
(세그먼트 트리를 사용할 때는 i를 반드시 1부터 시작하도록 하자. 그래야 죽지 않고 오래 산다)
그러면 일반적인 방식으로는 4 + 3 + 7 + 2 + 1 이런식으로 구한다.
하지만, 세그먼트 트리 방식을 이용하면 7 + 9 + 1 이런식으로 구할 수 있다.
조회해야하는 대상이 2배씩 줄어드는 관계가 보인다! 그러므로 시간 복잡도를 O(N)에서 O(logN)으로 줄일 수 있다.
그러면 이제 7이 적힌 노드와 9가 적힌 노드를 찾으면 되는 것인데
그걸 어떻게 찾냐면,완전 이진 트리의 특성으로 찾을 수 있다.
노드번호를 이런 방식으로 할당하면, 어떠한 관계가 관찰된다.

x번호인 노드의 왼쪽 자식 노드는 2* x 번호를 갖는다.
x번호인 노드의 오른쪽 자식 노드는 2* x + 1번호를 갖는다.
x번호의 노드의 부모 노드는 x/2의 번호를 갖는다.
그러면 i=3~7(1 based index)까지의 구간합을 구하겠다는 것은
노드 10번 ~14번까지의 합을 구하겠다는 것과 같고
그것은 SUM(노드 5번,노드 6번,노드 14번)을 구하겠다는 것과 같다.
이를 관계로 표현하면,
i = start ~ end까지의 구간합을 구하겠다는 것은 start + N - 1번 ~ end + N -1번까지의 합을 구하겠다는 것과 같다.
이를 어떻게 구할까.
start + N - 1번 ~ end + N -1번까지의 합을 구했어야 했다. 그걸 start_index ~ end_index라고 하자.
(start_index = start + N - 1;
end_index = end + N - 1; )
우리가 위에서 노드 10번 ~ 14번까지의 합을 구하는건 노드 5번 노드6번 노드14번의 합을 구하는 것이라고 했다.
그런데 우리가 원하는 합을 구하는 방식은 O(N)의 시간복잡도가 아니다. O(logN)의 시간복잡도를 원한다.
그러려면 10,11,12,13,14를 전부 순회하면 안된다. 5,6,14번만 순회하면 된다.
즉, 10~14번까지 순회해야한다면 5번과 6번 14번만 순회하면 된다.
이걸 일반화 해보자. 10을 start_index로 보고 14를 end_index로 보자.
start_index~end_index까지 순회해야한다면, start_index / 2번, (end_index - 1) / 2번, end_index번을 순회하면 된다.
하지만 이건 제대로 일반화하진 못했다.

start_index가 9,end_index가 14라고 하면 노드 9번 노드 5번 노드 6번 노드 14번의 합이 답이므로
이걸 일반화하면 start_index번, (start_index + 1) / 2번, (end_index - 1) / 2번, end_index번을 순회하면 된다.
잘 살펴보면 start_index, end_index가 짝수이거나 홀수일때에 따라 상황이 달라짐을 알 수 있다.
이를 일반화하면 start_index가 홀수라면 start_index번호와 (start_index + 1) / 2번호가 정답의 원소가 된다.
start_index가 짝수라면 start_index / 2 번호가 정답의 원소가 된다.
end_index가 짝수라면 (end_index - 1) / 2번, end_index번호가 정답의 원소가 된다.
end_index가 홀수라면 end_index / 2 번호가 정답의 원소가 된다.
이런식으로 진행된다.
long getSum(int s, int e) { // 구간합 연산 함수
long partSum = 0;
while (s <= e) {
if (s % 2 == 1) {
partSum = partSum + tree[s];
s++;
}
if (e % 2 == 0) {
partSum = partSum + tree[e];
e--;
}
s = s / 2;
e = e / 2;
}
return partSum;
}이걸 정리하면,
1) start_index % 2 == 1일 때 해당 노드를 선택하고 start_index = start_index + 1로 갱신
2) end_index % 2 == 0일 때 해당 노드를 선택하고 end_index = end_index - 1로 갱신
3) start_index = start_index / 2를실행함
4) end_index= end_index / 2를 실행함
5) 1)~4)를 반복, end_index <start_index가 되면 종료함
그러면
| start | end |
|---|---|
| 9 | 14 |
| 5 | 6 |
| 3 | 2 |
| 이렇게 된다. 5 6 에서 3 2로 가는 단계에서, 위치가 크로스 되면서 멈춘다. |
데이터 업데이트 하기
데이터를 업데이트한 다음에도 세그먼트 트리를 통한 질의 결과 값을 계속 도출하고 싶으면
당연히 트리또한 업데이트를 해줘야 할 것이다. 이 부분에서 이해하기 어려운 건 전혀 없다!
배열의 원소중 7을 10으로 업데이트 해준다고 하면... 3이 증가한 것이다.
7의 부모노드, 7의 부모노드의 부모노드, ... 를 전부 3 증가시키면 된다.

void changeVal(int index, long val) { // 트리 값 변경 함수
long diff = val - tree[index];
while (index > 0) {
tree[index] = tree[index] + diff;
index = index / 2;
}
}문제 15678번 연세워터파크
문제를 요약하면 이런 문제다.
징검다리를 건너는데 가능한 최대 점수를 출력하는 문제이다.
시작지점은 어느 징검다리가 될 수도 있다.
징검다리에서 빠져 나올 때 아무때나 나오고 싶을 때 나올 수 있다.
D=2면 최대 2칸까지 점프가 가능하다. 징검 다리는 한번만 밟을 수 있다.
아무때나 나오고 싶을 때 나올 수 있으므로, 각 지점에 도착을 했을 때 최대점수를 구하면 되겠지? 이런 생각이 들 것이다.
그렇게 i=0 ~ i=n-1번 징검다리에 도착했을 때 최대점수를 다 구하고 그 중에서 다시 max를 구하면 되어보인다.
여기서 DP를 떠올릴 수 있다.
i=k라고 하면 k위치에 도착했을 때 최대점수를 구하는 건 i!=k인 모든 지점에서 도착했을때 최대점수에서 k위치로 이동하는 것이다.
이전 계산 결과를 재활용하여 계산이 가능하므로 DP계산이 가능하다.dp[k]의 후보는 dp[k를 제외한 모든 요소]라고 범위를 러프하게 좁힐 수 있다. 그런데 여기서 D가 존재하므로 범위가 더 좁아진다.
k=1이라면 k-1, k+1만 가능할 것이고, k=2면 k-2,k-1,k+1,k+2가 가능하다.
그런데, D[k]를 구할 때 여기서 또 k+1이나 k+1,k+2인 경우는 고려하지 않아도 된다. 왜냐하면 대칭성 때문이다.
궁극적으로는 D[1] ~D[n-1]까지의 DP값중에서 가장 큰 값을 고른다. 그렇기 때문에, k+1,k+2인 경우는 고려하지 않아도 된다.
왜요?! dp테이블에 값이 확연히 달라지잖아요! 그렇다. 딱 k인 상황만 보면 그렇다.
그러면 그 상황을 보자. 만약에 1....k-1까지는 음수이고 k, k+1,k+2만 양수라고 하자.
그러면 k+1,k+2에 의해 dp[k]가 최댓값이 될 것이다. 그런데 딱 보면, dp[k]도 dp[k+1]도 dp[k+2]도 다 같은 최댓값이 될 것이다.
즉, 중복 계산이 되는 것이다.
k+1,k+2 방향을 고려하지 않아도 되는 이유는 이것이다.
k에서 k+1로 가고 k+2로 가는 그 route의 값은 dp[k]에서 고려해주지 않아도 dp[k+2]에서 고려될 것이다.
즉, 단방향만 고민하면 된다.
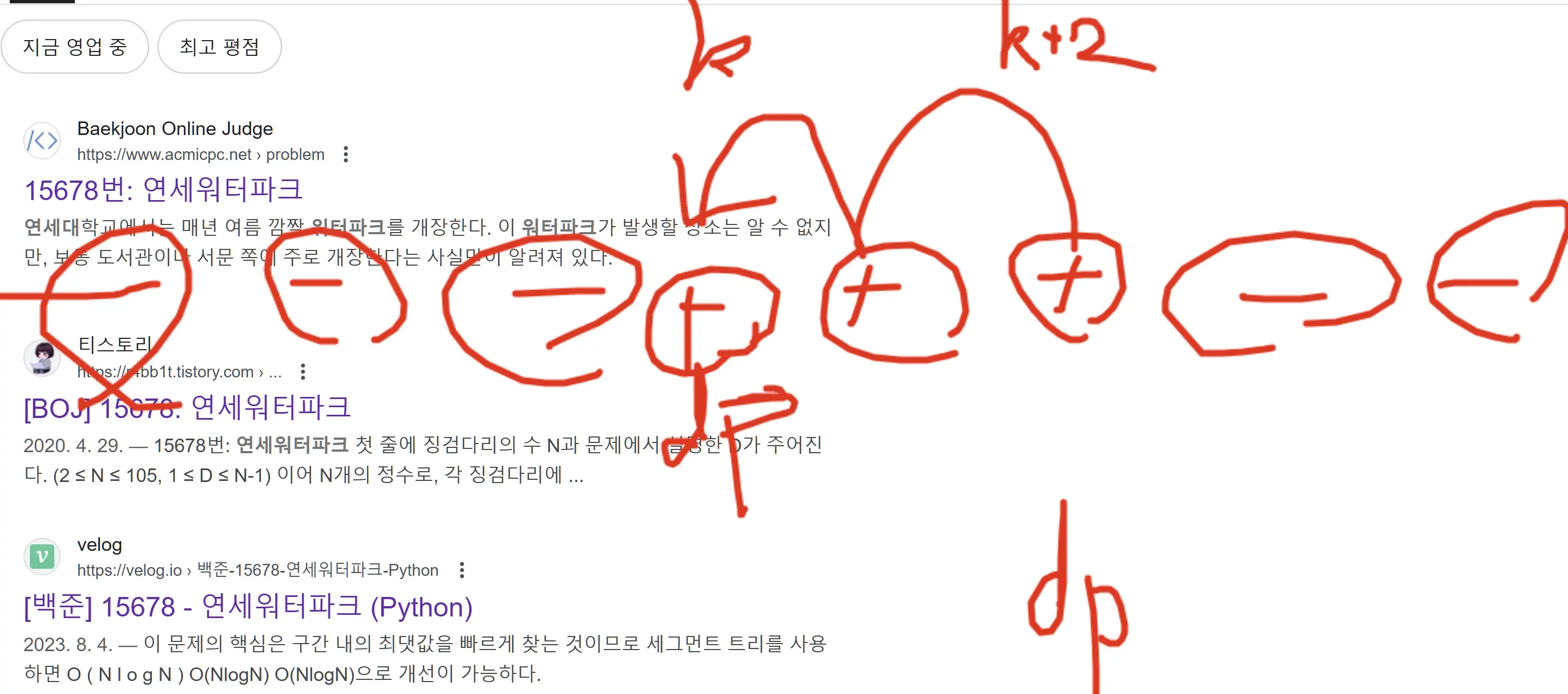
그러면 dp[k]는 dp[k-d~k-1]까지만 고려하면 된다.
dp[i]=max(K[i], max(DP[j]) + k[i]) for j∈[max(0, i−d),i−1]
이런 식의 점화식이 세워진다.
또는DP[i]=max(K[i],max(DP[i−D],...,DP[i−1])+K[i])(i - D>= 0)
이런 식의 점화식이 세워진다.
왜 max(0,i-d)이냐면 i가 음수인 경우는 고려하지 않아도 되기 때문이다. D=5일 때
5번을 한번에 점프할 수 있어도 시작위치는 -3 이런건 불가능하고 0부터 가능하기때문이다.
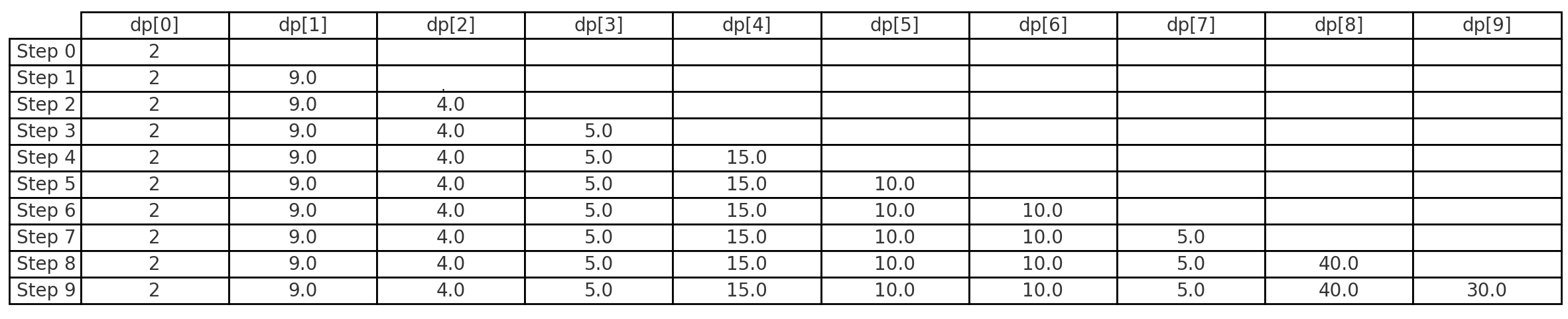
dp[i]테이블이 갱신되면 트리도 갱신되야 하므로 update를 진행한다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;
vector<long long> Tree; vector<long long> DP; vector<long long> K;
// void set_tree(int size) { // 1 based Tree
// for (int i = size - 1; i >= 1; i--) {
// Tree[i] = Tree[2 * i] + Tree[2 * i + 1];// [i] = [2i] + [2i + 1]
// }
// }
long long get_max(int size, int l, int r) {
long long max_value = LLONG_MIN;
l += size;
r += size;
while (l <= r) {
if (l % 2) max_value = max(max_value, Tree[l++]);
if (!(r % 2)) max_value = max(max_value, Tree[r--]);
l /= 2;
r /= 2;
}
return max_value;
}
void update(int size, int i, long long value) {
i += size;
Tree[i] = value;
while (i > 1) {
i /= 2;
Tree[i] = max(Tree[i * 2], Tree[i * 2 + 1]);
}
}
int main() {
int n, d;
cin >> n >> d;
int size = 1;
while (size < n) size *= 2;
Tree.resize(2 * size, LLONG_MIN);
K.resize(n);
DP.resize(n, 0);
for (int i = 0; i < n; i++) {
cin >> K[i];
DP[i] = K[i];
}
long long result = LLONG_MIN;
for (int i = 0; i < n; i++) {
long long max_prev = 0;
//0은 예외 i-d ~ i-1까지 세그먼트트리로 max 구하기
if (i > 0) max_prev = get_max(size, max(0, i - d), i - 1);
DP[i] = max(K[i], K[i] + max_prev);
update(size, i, DP[i]);
result = max(result, DP[i]);
}
cout << result << "\n";
return 0;
}
Principle of Optimality
Principle of Optimality를 생각해보자. 부분 문제가 최적해가 아닌데
전체 문제가 최적해인 경우가 있다고 가정하자.
즉, k-1번째 징검다리로 도착하는 최대점수가 최적해가 아니면서
k번째 징검다리로 도착하는 최대점수의 최적해가 있다고 가정하자.
k번째 징검다리로 도착하는 최대 점수를 얻기 위해 k-1 번째 징검다리로 도착하는 최대점수를 사용했다.
그런데 k-1번째 징검다리로 도착하는 최대점수가 최적해가 아니라면
그걸 최적해로 교체하는 경우가 있다는 것이다.
그렇다면 k번째 징검다리로 도착하는 최대 점수 또한 최적해가 아니다.
가정에서 k번째 징검다리로 도착하는 최대점수가 최적해라고 가정했으므로 모순이 발생한다.
'알고리즘' 카테고리의 다른 글
| 백준 32350번 오버킬(overkill) 문제풀이 (1) | 2025.01.14 |
|---|---|
| 알고리즘 문풀 : 2023 KAKAO BLIND RECRUITMENT 개인정보 수집 유효기간 (2) | 2025.01.13 |
| 백준 2252 줄 세우기 (위상정렬) (2) | 2025.01.13 |
| 다익스트라, 벨만포드 알고리즘 (1) | 2024.12.23 |
| 백준 32714번 방벽게임 (0) | 2024.11.27 |
세그먼트 트리
세그먼트 트리는 배열의 데이터에 대한 구간 질의(구간합, 최대,최소, 구간곱),
배열 값 업데이트를 빠르게 수행하기 위해 고안해 낸자료구조이다.
세그먼트 트리는 완전 이진 트리로 구현한다.
세그먼트 트리 이해하기
샘플 데이터 {5, 8, 4, 3, 7, 2, 1, 6}가 있다. N = 8 (배열의 크기, 트리배열의 크기도 8이다)
그리고 그 샘플 데이터로 만든 배열 위에 세그먼트 트리를 그려보았다.

질의 결과 값 구하기
i=1부터 시작한다고 가정했을 때, i=3~7까지의 합이 구간 질의로 주어졌다고 하자.
(세그먼트 트리를 사용할 때는 i를 반드시 1부터 시작하도록 하자. 그래야 죽지 않고 오래 산다)
그러면 일반적인 방식으로는 4 + 3 + 7 + 2 + 1 이런식으로 구한다.
하지만, 세그먼트 트리 방식을 이용하면 7 + 9 + 1 이런식으로 구할 수 있다.
조회해야하는 대상이 2배씩 줄어드는 관계가 보인다! 그러므로 시간 복잡도를 O(N)에서 O(logN)으로 줄일 수 있다.
그러면 이제 7이 적힌 노드와 9가 적힌 노드를 찾으면 되는 것인데
그걸 어떻게 찾냐면,완전 이진 트리의 특성으로 찾을 수 있다.
노드번호를 이런 방식으로 할당하면, 어떠한 관계가 관찰된다.

x번호인 노드의 왼쪽 자식 노드는 2* x 번호를 갖는다.
x번호인 노드의 오른쪽 자식 노드는 2* x + 1번호를 갖는다.
x번호의 노드의 부모 노드는 x/2의 번호를 갖는다.
그러면 i=3~7(1 based index)까지의 구간합을 구하겠다는 것은
노드 10번 ~14번까지의 합을 구하겠다는 것과 같고
그것은 SUM(노드 5번,노드 6번,노드 14번)을 구하겠다는 것과 같다.
이를 관계로 표현하면,
i = start ~ end까지의 구간합을 구하겠다는 것은 start + N - 1번 ~ end + N -1번까지의 합을 구하겠다는 것과 같다.
이를 어떻게 구할까.
start + N - 1번 ~ end + N -1번까지의 합을 구했어야 했다. 그걸 start_index ~ end_index라고 하자.
(start_index = start + N - 1;
end_index = end + N - 1; )
우리가 위에서 노드 10번 ~ 14번까지의 합을 구하는건 노드 5번 노드6번 노드14번의 합을 구하는 것이라고 했다.
그런데 우리가 원하는 합을 구하는 방식은 O(N)의 시간복잡도가 아니다. O(logN)의 시간복잡도를 원한다.
그러려면 10,11,12,13,14를 전부 순회하면 안된다. 5,6,14번만 순회하면 된다.
즉, 10~14번까지 순회해야한다면 5번과 6번 14번만 순회하면 된다.
이걸 일반화 해보자. 10을 start_index로 보고 14를 end_index로 보자.
start_index~end_index까지 순회해야한다면, start_index / 2번, (end_index - 1) / 2번, end_index번을 순회하면 된다.
하지만 이건 제대로 일반화하진 못했다.

start_index가 9,end_index가 14라고 하면 노드 9번 노드 5번 노드 6번 노드 14번의 합이 답이므로
이걸 일반화하면 start_index번, (start_index + 1) / 2번, (end_index - 1) / 2번, end_index번을 순회하면 된다.
잘 살펴보면 start_index, end_index가 짝수이거나 홀수일때에 따라 상황이 달라짐을 알 수 있다.
이를 일반화하면 start_index가 홀수라면 start_index번호와 (start_index + 1) / 2번호가 정답의 원소가 된다.
start_index가 짝수라면 start_index / 2 번호가 정답의 원소가 된다.
end_index가 짝수라면 (end_index - 1) / 2번, end_index번호가 정답의 원소가 된다.
end_index가 홀수라면 end_index / 2 번호가 정답의 원소가 된다.
이런식으로 진행된다.
long getSum(int s, int e) { // 구간합 연산 함수
long partSum = 0;
while (s <= e) {
if (s % 2 == 1) {
partSum = partSum + tree[s];
s++;
}
if (e % 2 == 0) {
partSum = partSum + tree[e];
e--;
}
s = s / 2;
e = e / 2;
}
return partSum;
}이걸 정리하면,
1) start_index % 2 == 1일 때 해당 노드를 선택하고 start_index = start_index + 1로 갱신
2) end_index % 2 == 0일 때 해당 노드를 선택하고 end_index = end_index - 1로 갱신
3) start_index = start_index / 2를실행함
4) end_index= end_index / 2를 실행함
5) 1)~4)를 반복, end_index <start_index가 되면 종료함
그러면
| start | end |
|---|---|
| 9 | 14 |
| 5 | 6 |
| 3 | 2 |
| 이렇게 된다. 5 6 에서 3 2로 가는 단계에서, 위치가 크로스 되면서 멈춘다. |
데이터 업데이트 하기
데이터를 업데이트한 다음에도 세그먼트 트리를 통한 질의 결과 값을 계속 도출하고 싶으면
당연히 트리또한 업데이트를 해줘야 할 것이다. 이 부분에서 이해하기 어려운 건 전혀 없다!
배열의 원소중 7을 10으로 업데이트 해준다고 하면... 3이 증가한 것이다.
7의 부모노드, 7의 부모노드의 부모노드, ... 를 전부 3 증가시키면 된다.

void changeVal(int index, long val) { // 트리 값 변경 함수
long diff = val - tree[index];
while (index > 0) {
tree[index] = tree[index] + diff;
index = index / 2;
}
}문제 15678번 연세워터파크
문제를 요약하면 이런 문제다.
징검다리를 건너는데 가능한 최대 점수를 출력하는 문제이다.
시작지점은 어느 징검다리가 될 수도 있다.
징검다리에서 빠져 나올 때 아무때나 나오고 싶을 때 나올 수 있다.
D=2면 최대 2칸까지 점프가 가능하다. 징검 다리는 한번만 밟을 수 있다.
아무때나 나오고 싶을 때 나올 수 있으므로, 각 지점에 도착을 했을 때 최대점수를 구하면 되겠지? 이런 생각이 들 것이다.
그렇게 i=0 ~ i=n-1번 징검다리에 도착했을 때 최대점수를 다 구하고 그 중에서 다시 max를 구하면 되어보인다.
여기서 DP를 떠올릴 수 있다.
i=k라고 하면 k위치에 도착했을 때 최대점수를 구하는 건 i!=k인 모든 지점에서 도착했을때 최대점수에서 k위치로 이동하는 것이다.
이전 계산 결과를 재활용하여 계산이 가능하므로 DP계산이 가능하다.dp[k]의 후보는 dp[k를 제외한 모든 요소]라고 범위를 러프하게 좁힐 수 있다. 그런데 여기서 D가 존재하므로 범위가 더 좁아진다.
k=1이라면 k-1, k+1만 가능할 것이고, k=2면 k-2,k-1,k+1,k+2가 가능하다.
그런데, D[k]를 구할 때 여기서 또 k+1이나 k+1,k+2인 경우는 고려하지 않아도 된다. 왜냐하면 대칭성 때문이다.
궁극적으로는 D[1] ~D[n-1]까지의 DP값중에서 가장 큰 값을 고른다. 그렇기 때문에, k+1,k+2인 경우는 고려하지 않아도 된다.
왜요?! dp테이블에 값이 확연히 달라지잖아요! 그렇다. 딱 k인 상황만 보면 그렇다.
그러면 그 상황을 보자. 만약에 1....k-1까지는 음수이고 k, k+1,k+2만 양수라고 하자.
그러면 k+1,k+2에 의해 dp[k]가 최댓값이 될 것이다. 그런데 딱 보면, dp[k]도 dp[k+1]도 dp[k+2]도 다 같은 최댓값이 될 것이다.
즉, 중복 계산이 되는 것이다.
k+1,k+2 방향을 고려하지 않아도 되는 이유는 이것이다.
k에서 k+1로 가고 k+2로 가는 그 route의 값은 dp[k]에서 고려해주지 않아도 dp[k+2]에서 고려될 것이다.
즉, 단방향만 고민하면 된다.

그러면 dp[k]는 dp[k-d~k-1]까지만 고려하면 된다.
dp[i]=max(K[i], max(DP[j]) + k[i]) for j∈[max(0, i−d),i−1]
이런 식의 점화식이 세워진다.
또는DP[i]=max(K[i],max(DP[i−D],...,DP[i−1])+K[i])(i - D>= 0)
이런 식의 점화식이 세워진다.
왜 max(0,i-d)이냐면 i가 음수인 경우는 고려하지 않아도 되기 때문이다. D=5일 때
5번을 한번에 점프할 수 있어도 시작위치는 -3 이런건 불가능하고 0부터 가능하기때문이다.
dp[i]테이블이 갱신되면 트리도 갱신되야 하므로 update를 진행한다.

#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;
vector<long long> Tree; vector<long long> DP; vector<long long> K;
// void set_tree(int size) { // 1 based Tree
// for (int i = size - 1; i >= 1; i--) {
// Tree[i] = Tree[2 * i] + Tree[2 * i + 1];// [i] = [2i] + [2i + 1]
// }
// }
long long get_max(int size, int l, int r) {
long long max_value = LLONG_MIN;
l += size;
r += size;
while (l <= r) {
if (l % 2) max_value = max(max_value, Tree[l++]);
if (!(r % 2)) max_value = max(max_value, Tree[r--]);
l /= 2;
r /= 2;
}
return max_value;
}
void update(int size, int i, long long value) {
i += size;
Tree[i] = value;
while (i > 1) {
i /= 2;
Tree[i] = max(Tree[i * 2], Tree[i * 2 + 1]);
}
}
int main() {
int n, d;
cin >> n >> d;
int size = 1;
while (size < n) size *= 2;
Tree.resize(2 * size, LLONG_MIN);
K.resize(n);
DP.resize(n, 0);
for (int i = 0; i < n; i++) {
cin >> K[i];
DP[i] = K[i];
}
long long result = LLONG_MIN;
for (int i = 0; i < n; i++) {
long long max_prev = 0;
//0은 예외 i-d ~ i-1까지 세그먼트트리로 max 구하기
if (i > 0) max_prev = get_max(size, max(0, i - d), i - 1);
DP[i] = max(K[i], K[i] + max_prev);
update(size, i, DP[i]);
result = max(result, DP[i]);
}
cout << result << "\n";
return 0;
}
Principle of Optimality
Principle of Optimality를 생각해보자. 부분 문제가 최적해가 아닌데
전체 문제가 최적해인 경우가 있다고 가정하자.
즉, k-1번째 징검다리로 도착하는 최대점수가 최적해가 아니면서
k번째 징검다리로 도착하는 최대점수의 최적해가 있다고 가정하자.
k번째 징검다리로 도착하는 최대 점수를 얻기 위해 k-1 번째 징검다리로 도착하는 최대점수를 사용했다.
그런데 k-1번째 징검다리로 도착하는 최대점수가 최적해가 아니라면
그걸 최적해로 교체하는 경우가 있다는 것이다.
그렇다면 k번째 징검다리로 도착하는 최대 점수 또한 최적해가 아니다.
가정에서 k번째 징검다리로 도착하는 최대점수가 최적해라고 가정했으므로 모순이 발생한다.
'알고리즘' 카테고리의 다른 글
| 백준 32350번 오버킬(overkill) 문제풀이 (1) | 2025.01.14 |
|---|---|
| 알고리즘 문풀 : 2023 KAKAO BLIND RECRUITMENT 개인정보 수집 유효기간 (2) | 2025.01.13 |
| 백준 2252 줄 세우기 (위상정렬) (2) | 2025.01.13 |
| 다익스트라, 벨만포드 알고리즘 (1) | 2024.12.23 |
| 백준 32714번 방벽게임 (0) | 2024.11.27 |
